C++ : POLICY BASED DATA STRUCTES
Whether you’re solving brain-teasers in a coding contest or building the next big software, the right data structures can mean the difference between “nailed it” and “why is this still running?!”
Think of the Standard Template Library (STL) as your trusty toolbox. It’s got the hammers, screwdrivers, and wrenches you need for most jobs. But what about those times when you need a laser cutter or a 3D printer? That’s where GNU C++ PBDS (Policy-Based Data Structures) comes in—it’s the advanced arsenal that turns you from a good coder into a coding superhero.
GNU C++ PBDS (Policy-Based Data Structures) is a powerful extension of STL that introduces a variety of advanced data structures, perfect for competitive programming and C++ development. With features like order statistics, dynamic range queries, and priority queue optimizations, PBDS enables you to tackle problems with efficiency and elegance. Whether you need to efficiently find the k-th smallest element, maintain dynamic order statistics, or handle graph algorithms with ease, PBDS has you covered.
In this blog, we’ll dive into the key components of PBDS, showcasing practical examples and exploring the real-world benefits of using these advanced data structures.
pb_ds : The Hidden Gem
- Efficiency Boost: Say goodbye to writing custom data structures from scratch.
- Versatility: Handle complex operations like order statistics, range queries, and priority updates effortlessly.
- Compact Syntax: Write less, achieve more.
Here are some scenarios where pb_ds shines:
- Finding the k-th smallest/largest element
- Prefix-based search and string matching
- Efficient handling of graph algorithms like Dijkstra’s or Prim’s
The underlying data-structures currently supported in pb_ds are :
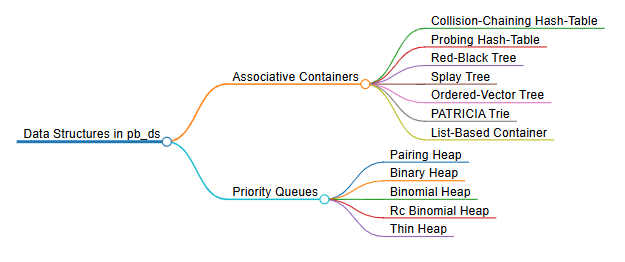
Let’s discuss a few of them, we will focus on how these data structures can be useful to us in solving real-world problems and competitive programming challenges, rather than diving into the internal details of their implementations.yy
Key Components of pb_ds
1. Tree-Based Containers
Let’s talk about the star of the show : ordered_set, implemented as a red-black tree with extended functionality. These containers are perfect for problems involving dynamic order statistics or range queries.
Usage
To use this data-structure :
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace __gnu_pbds;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> ordered_set;
Methods
Other than the standard std::set methods, ordered_set also offers some other methods:
find_by_orderorder_of_key
Time Complexity : O(log(n))
Example :
int main(){
ordered_set s;
s.insert(2);
s.insert(9);
s.insert(3);
// Count elements less than a given value
cout << s.order_of_key(9) << "\n"; //Outputs 2
// Find k-th smallest element (2nd smallest acc to 0-based indexing)
cout << *(s.find_by_order(1)) << "\n"; //Outputs 3
}
There’s also the ordered_multiset that is commonly implemented one of the two ways :
- Use an ordered_set of pairs to count occurences in
p.second. - Use the comparison operator
less_equal<data_type>. (Note that this exchanges the two functionss.lower_bound(x)ands.upper_bound(x)).
Applications of ordered_set :
- Inversion Count: Count the number of inversions in an array efficiently.
- Median Maintenance: Dynamically track the median in a stream of numbers.
- Range Counting: Count the number of elements in a specific range.
Above we have discussed about the order-statistics tree implemented by the red-black trees. A general tree from PBDS is discussed below.
We can define a tree as :
template<
typename Key, // Key type
typename Mapped, // Mapped-policy
typename Cmp_Fn = std::less<Key>, // Key comparison function
typename Tag = rb_tree_tag, // Inner Data structure
typename Node_Update = null_node_update, // Node update policy
typename Allocator = std::allocator<char> // Allocator type
> class tree;
- Keeping the
Mapped-policytonull_typedeclares aset. Otherwise it creates amap. Tagspecifies the underlying data structure. It can be among these :rb_tree_tag(default) = red-black treesplay_tree_tag= splay treeov_tree_tag= ordered-vector tree
Node_Updateis the policy which takes care of internal node invariants.null_node_update(default), memory efficienttree_order_statistics_node_update, enables the order-statistic methods :find_by_orderandorder_of_key.
For more , refer the official documentation at tree Interface and tree Design.
More Methods :
Even without the tree_order_statistics_node_update policy, PBDS trees support :
JoinSplit
Time Complexity : O(log(n))
Examples can be found at : 1 , 2
Observations :
rb_tree_tagis the most efficient for order-statistic methods. (reference)ov_tree_tagis the most efficient forsplitandjoinmethods.(reference)
2. Hash-Based Containers
Many of us have experienced the frustration of unordered_map underperforming in certain scenarios. Despite its theoretical efficiency, the constant factors involved sometimes slow down the performance considerably. (which may lead to an unexpected TLE in competitive programming). Hash-based containers in pb_ds, such as gp_hash_table are designed for ultra-fast operations with lower memory consumption.
These containers are designed like std::unordered_map and offer more flexibility, better performance with certain workloads, and the ability to use custom hash functions as well as resize_policy. We can get around get 2x to 5x improvement in execution time. The relevant tests can be found here.
The primary types of hash-based containers in PBDS are:
gp_hash_table– General-probing hash table.cc_hash_table– Collision-chaining hash table.
Why PBDS Hash Tables Outshine std::unordered_map
| Feature | std::unordered_map |
PBDS Hash Tables |
|---|---|---|
| Speed | Moderate | Lightning Fast |
| Memory Efficiency | High Overhead | Optimized |
| Customizability | Limited | Flexible (hash/resizing) |
| TLE Risk in Competitive Programming | High | Low |
Usage
To use this data-structure :
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/hash_policy.hpp>
using namespace __gnu_pbds;
typedef cc_hash_table<int, int> cc_table;
typedef gp_hash_table<int, int> gp_table;
Specifications
- Collision-chaining hash tables (cc_hash_table) offer better flexibility and timing performance because of their internal structure. They handle memory less efficiently than probing containers but are preferred for general use cases.
- General Probing container (gp_hash_table), on the other hand, are more memory-efficient, especially for simple data types.
- They are also advantageous in multi-threaded applications due to reduced memory allocation contention.
- For operations like eliminating duplicates or counting occurrences, probing containers might be more efficient.
Examples
1) gp_hash_table with a custom hash function
// Custom hash function
struct CustomHash {
size_t operator()(const std::string& key) const {
size_t hash = 0;
for (char c : key) {
hash = hash * 31 + c; // Simple polynomial hash
}
return hash;
}
};
int main() {
// Define a gp_hash_table mapping strings to integers
gp_hash_table<std::string, int, CustomHash> my_table;
my_table["one"] = 1;
my_table["two"] = 2;
for (const auto& pair : my_table) {
std::cout << pair.first << ": " << pair.second << "\n";
}
return 0;
}
2) gp_hash_table with resize policy
The code can be found in the repository.
3) The solution to this problem is analysed in this blog
It depicts faster time and AC solution when gp_hash_table is used in place of std::unordered_map.
3. Better Priority Queues
The priority queue alternative offered by pb_ds outperforms the STL’s std::priority_queue in terms of flexibility and time complexity.
The priority queue alternative offered by pb_ds outperforms the STL’s std::priority_queue in terms of flexibility and time complexity.
While std::priority_queue is based on a binary heap, GNU pb_ds gives you immense freedom by offering multiple underlying implementations, each tailored to different scenarios. The available tags for priority queues include:
pairing_heap: Pairing heap (self-adjusting heap with tree structure).binary_heap: Binary heap (complete binary tree).binomial_heap: Binomial heap (collection of binomial trees linked together).rc_binomial_heap: Relaxed binomial heap (variation of binomial heap with relaxed constraints).thin_heap: Thin heap (space-efficient variation of Fibonacci heap).
The default tag is binary_heap_tag.
Each of these implementations comes with its own perks and specific use cases, offering better alternatives to STL’s priority_queue.
Usage
#include <ext/pb_ds/priority_queue.hpp>
using namespace __gnu_pbds;
// replace thin_heap with the <tag> of your choice
typedef priority_queue<int, less<int>, thin_heap_tag> myPQ;
Methods
Other than the standard std::priority_queue methods, pb_ds also offers some other methods :
modifyerasejoinsplit
Dealing with Datatype <string>
- pairing_heap offers the best time and memory performance for push and pop operations. (reference : 1, 2, 3)
- join method: binomial_heap tag is the best for to join operations on multiple priority queues. (4).
- modification : pairing_heap for decrease_key method (5) and thin_heap for increase_key method (6).
For Datatype <integer>
Using the binary_heap (default) PBDS priority_queue would be better due to its efficiency in handling common operations like push and pop.
Tests for the same can be found at (7), (8).
The following table shows the complexities of the different underlying data structures in terms of orders of growth.
| priority_queue (tags) | push | pop | modify | erase | join |
|---|---|---|---|---|---|
| std : : priority_queue | Θ(n) worst & Θ(log(n)) amortized |
Θ(log(n)) worst |
Θ(nlog(n)) worst |
Θ(nlog(n)) |
Θ(nlog(n)) |
| pairing_heap_tag | O(1) |
Θ(n) worst & Θ(log(n)) amortized |
Θ(n) worst & Θ(log(n)) amortized |
Θ(n) worst & Θ(log(n)) amortized |
O(1) |
| binary_heap_tag | Θ(n) worst & Θ(log(n)) amortized |
Θ(n) worst & Θ(log(n)) amortized |
Θ(n) |
Θ(n) |
Θ(n) |
| binomial_heap_tag | Θ(log(n)) worst & O(1) amortized |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
| rc_binomial_heap_tag | O(1) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
| thin_heap_tag | O(1) |
Θ(n) worst & Θ(log(n)) amortized |
Θ(log(n)) worst & Θ(1) amortized |
Θ(n) worst & Θ(log(n)) amortized |
Θ(n) |
Reference : (9)
Examples
1) Modify Method
int main() {
typedef __gnu_pbds::priority_queue<int, std::less<int>, binary_heap_tag> PQ;
PQ pq;
PQ::point_iterator it = pq.push(15);
pq.push(10);
pq.push(5);
// Modify the element 15 to 7
pq.modify(it, 7);
// Output the elements after modification
while (!pq.empty()) {
std::cout << pq.top() << " ";
pq.pop();
}
// Output: 10 7 5
return 0;
}
2) Join Method
pb_ds supports merging two priority queues of the same type, which is especially useful in scenarios like graph algorithms.
int main() {
typedef __gnu_pbds::priority_queue<int, std::less<int>, binomial_heap_tag> PQ;
PQ pq1, pq2;
pq1.push(10);
pq1.push(20);
pq2.push(15);
pq2.push(25);
// Merge pq2 into pq1 using binomial heap join
pq1.join(pq2);
// To verify the above method
while (!pq1.empty()) {
std::cout << pq1.top() << " ";
pq1.pop();
}
// Output: 25 20 15 10
return 0;
}
3.) Priority Queue Split and Join example.
4. Trie-Based Containers
PBDS supports trie-based containers for prefix-based searches, longest-prefix matching, and other trie-centric algorithms. Unlike std::map or std::unordered_map, trie containers are optimized for hierarchical or lexicographical keys.
Tries are particularly useful for:
- Prefix-based searches: If you’re working with autocompletion systems or word suggestion algorithms, Tries are excellent for efficiently finding all words that share a common prefix.
- String matching: Tries can be employed in algorithms where you need to find specific patterns in a large set of strings.
Usage
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/trie_policy.hpp>
using namespace __gnu_pbds;
// To define the trie-based set container with prefix search
typedef trie<string, null_type, trie_string_access_traits<>, pat_trie_tag, trie_prefix_search_node_update> trie_set;
// To define the trie-based map container
typedef trie<string, int, trie_string_access_traits<>, pat_trie_tag, null_trie_node_update> trie_map;
You can look more into it at this link.
PATRICIA Tries
Patricia tries (practical prefix trees) optimize space usage by collapsing non-branching paths into single nodes.
- Trie-Based Set (trie_set): This container allows you to store keys, where the keys are stored in a Trie structure. The Trie guarantees that common prefixes are stored only once, resulting in a more compact representation.
- Trie-Based Map (trie_map): Similar to the Trie-based set, but instead of just storing keys, this container also stores values associated with each key. This makes it ideal for situations where you need to store a mapping from a key to a value.
Patricia tries prove highly useful for :
- IP routing tables.
- Efficient prefix compression in strings.
- Fast substring matching.
Example
Using trie_set
int main() {
trie_set t;
// Insert elements
t.insert("apple");
t.insert("app");
t.insert("banana");
t.insert("bat");
// Search for a specific key
if (t.find("app") != t.end())
cout << "Found: app\n";
// Prefix search
auto range = t.prefix_range("ba");
for (auto it = range.first; it != range.second; ++it)
cout << "Prefix match: " << *it << "\n";
// Outputs "banana" and "bat"
return 0;
}
pb_ds in Action
1) Count Number of Inversions in an Array
Using ordered_set. Note the use of less_equal<int> comparator, essentially making it an ordered_multiset.
#include <bits/stdc++.h>
using namespace std;
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace __gnu_pbds;
typedef tree<int, null_type, less_equal<int>, rb_tree_tag, tree_order_statistics_node_update> ordered_set;
int countInversions(vector<int>& arr) {
ordered_set os;
int inversions = 0;
for (int i = arr.size() - 1; i >= 0; i--) {
inversions += os.order_of_key(arr[i]);
os.insert(arr[i]);
}
return inversions;
}
int main() {
vector<int> arr = {3, 1, 2};
cout << countInversions(arr) << endl; // Output: 2
return 0;
}
- Time Complexity :
O(nlogn) - Space Complexity :
O(n)
2) Shortest Path using Pairing Heap
The below code uses priority queue implemented using pairing heap.
#include <bits/stdc++.h>
using namespace std;
#include <ext/pb_ds/priority_queue.hpp>
using namespace __gnu_pbds;
using PairingHeap = __gnu_pbds::priority_queue<std::pair<int, int>, std::greater<std::pair<int, int>>, pairing_heap_tag>;
void dijkstra(int start, const std::vector<std::vector<std::pair<int, int>>>& graph) {
PairingHeap pq;
std::vector<int> dist(graph.size(), INT_MAX);
pq.push({0, start});
dist[start] = 0;
while (!pq.empty()) {
auto top = pq.top();
pq.pop();
int d = top.first, u = top.second;
if (d > dist[u]) continue;
for (const auto& neighbor : graph[u]) {
int weight = neighbor.first, v = neighbor.second;
if (dist[u] + weight < dist[v]) {
dist[v] = dist[u] + weight;
pq.push({dist[v], v});
}
}
}
for (int i = 0; i < dist.size(); ++i) {
std::cout << "Distance to " << i << ": " << dist[i] << "\n";
}
}
int main() {
std::vector<std::vector<std::pair<int, int>>> graph(4);
graph[0].push_back( {1, 1} );
graph[0].push_back( {4, 2} );
graph[1].push_back( {1, 0} );
graph[1].push_back( {2, 2} );
graph[1].push_back( {6, 3} );
graph[2].push_back( {4, 0} );
graph[2].push_back( {2, 1} );
graph[2].push_back( {3, 3} );
graph[3].push_back( {6, 1} );
graph[3].push_back( {3, 2} );
dijkstra(0, graph);
return 0;
/* Output:
Distance to 0: 0
Distance to 1: 1
Distance to 2: 3
Distance to 3: 6
*/
}
The pb_ds pairing heap version of Dijkstra’s algorithm has a better amortized complexity O(V log V + E) than the traditional STL binary heap version O((V + E) log V). It performs particularly well in dense graphs and scenarios where decrease-key operations dominate.
3) Finding the Frequency of Elements in a Sliding Window
The gp_hash_table provides O(1) average time complexity for insertions, deletions, and lookups, making it well-suited for dynamic updates required in a sliding window problem.
#include <bits/stdc++.h>
using namespace std;
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/hash_policy.hpp>
using namespace __gnu_pbds;
// Define gp_hash_table
typedef gp_hash_table<int, int> hash_table;
void sliding_window_frequencies(const std::vector<int>& arr, int k) {
if (k > arr.size()) {
std::cout << "Window size is larger than the array size.\n";
return;
}
hash_table freq;
// Initialize the first window
for (int i = 0; i < k; ++i) {
freq[arr[i]]++;
}
// Output frequencies for the first window
std::cout << "Window [0, " << k - 1 << "]:\n";
for (const auto& pair : freq) {
std::cout << pair.first << ": " << pair.second << "\n";
}
// Slide the window
for (int i = k; i < arr.size(); ++i) {
int outgoing = arr[i - k]; // Element leaving the window
int incoming = arr[i]; // Element entering the window
// Decrease the count of the outgoing element
if (--freq[outgoing] == 0) {
freq.erase(outgoing);
}
// Increase the count of the incoming element
freq[incoming]++;
// Output frequencies for the current window
std::cout << "Window [" << i - k + 1 << ", " << i << "]:\n";
for (const auto& pair : freq) {
std::cout << pair.first << ": " << pair.second << "\n";
}
}
}
int main() {
std::vector<int> arr = {1, 2, 1, 3, 4, 7, 2, 4};
int k = 5;
sliding_window_frequencies(arr, k);
return 0;
}
These are some more examples of the class methods from the github repository.
Conclusion
pb_ds is a treasure trove for competitive programmers. It saves time, simplifies code, and enables you to focus on solving problems rather than debugging custom data structures. With its variety of priority queue implementations, tree-based containers, hash-based structures and many more, it’s a must-have tool in your arsenal. Thank you!
_Authors: Tattwa Shiwani, Khushi Ranawat
References :
- Official Documentation (link to files might be depricated, the files can be found in the repository below)
- Tests (some conclusions are drawn from these tests)
- Github Repository
- Codeforces Blog on Ordered Set
- Codeforces Blog on Hash Tables